Performance accademica: Alcuni risultati empirici

Performance accademica: Alcuni risultati empirici

Le informazioni a disposizione degli autori erano relative a 687 immatricolati nell’anno 2009 e ad una serie di indicatori di performance e di informazioni, relative all’iscrizione universitaria o all’abbandono degli studi entro il primo anno. Tutti gli studenti sono stati sottoposti ad un test di ingresso di tipo non selettivo (un test matematico basato su 20 domande a risposta multipla). Definiamo Y la variabile binaria che assume il valore 0 se lo studente continua gli studi e valore 1 se abbandona al primo anno. Sia X un vettore di regressori che si assume possa influenzare Y. Stimiamo la probabilità di abbandonare gli studi attraverso il modello probit:

P r(Y = 1|X) = ƒ(X’b)

con ƒ funzione di ripartizione della variabile casuale normale. Il vettore dei parametri b pu  essere stimato con il metodo della massima verosimiglianza. Sulla base delle informazioni empiriche a disposizione sono stati considerati 5 differenti criteri di selezione cioè 5 differenti definizioni del vettoreX:

1.    selezione basata sul solo voto di maturità (v): X = ln(v)
2.    selezione basata sul solo risultato del test (T): X = ln(T)
3.    selezione basata sulla scarto del voto di maturità rispetto la media del tipo di scuola di provenienza: X = ln(v) ln(v ?)
4.    selezione basata sia sul risultato del test che sul voto di maturità: X = ln(v), ln(T)
5.    selezione che considera tutte le informazioni disponibili:?

X = ln(v), ln(T), sesso, scuola secondaria, eta, residenza, sede

I risultati delle stime probit sono presentati nella Tabella 5.1 che riporta i valori stimati del vettore b, l’errore standard e la significatività.

Voti di maturità e risultati del test più alti portano ad una minore probabilità di abbandono. I coefficienti del voto di maturità sono generalmente più alti, in valore assoluto, di quelli del risultato del test. Questi coefficienti rappresentano le semi elasticità della probabilità di abbandonare gli studi, al voto e al risultato del test. Un aumento dell’1% del voto di maturità implica una riduzione della probabilità di abbandono compresa il 1.6% e il 2.2%, un aumento dell’1% del risultato del test è associato ad una riduzione della probabilità di abbandonare compresa tra l’1.2% e l’1.4%, a seconda delle differenti specificazioni del modello.

Le variabili relative alle caratteristiche individuali sono scarsamente rilevanti, il diploma in istituti differenti dal tecnico commerciale e la provenienza da altre regioni aumentano la probabilità di abbandono, l’età non è significativa.

Dalle stime della Tabella 4.1, per ognuna delle equazioni, possiamo calcolare i valori predetti delle stime della probabilità di drop-out (Y). Gli studenti possono quindi essere classificati

Tabella 4.1 Stime della probabilità di abbandonare gli studi al primo anno.

Diploma: riferimento Scientifico. 2 classico, 3 linguistico-magistrale, 4  tecnico, 5 commerciale, 6 professionale.          Età: riferimento minore di 19 anni 4 mesi. 2 tra 19a4m e 19a8m, 3 tra 19a8m e 20a, 4 20a, 5 21 a 22 a, 6 più di 22a.    Provenienza: riferimento Comune di Ancona. 2 Provincia di Ancona (comune), 3 provincia di Ascoli, provincia di Fermo, 5 provincia di Pesaro, 6 Abruzzo, 7 Altre regioni. [fonte: banca dati iscritti ed esami sostenuti, Corso di Laurea in Economia, Ancona] seconda della probabilità di abbandono.

Assumendo che la selezione venga fatta in modo da escludere per primi gli studenti con probabilità stimata di abbandono più alta, per ogni possibile tasso di ammissione dei candidati è possibile calcolare la quota di abbandoni (la relazione tra x e f(x) del modello teorico). Quanto più il processo di selezione è efficiente, tanto più questa quota deve essere bassa. La relazione tra tasso di ammissione (sulle ascisse) e tasso di drop-out (sulle ordinate) per 4 dei 5 metodi di selezione degli studenti (non viene qui riportato lo scarto dal voto medio di diploma perché non fornisce altre informazioni rispetto al solo voto di diploma), è riepilogato nella figura 4.1.

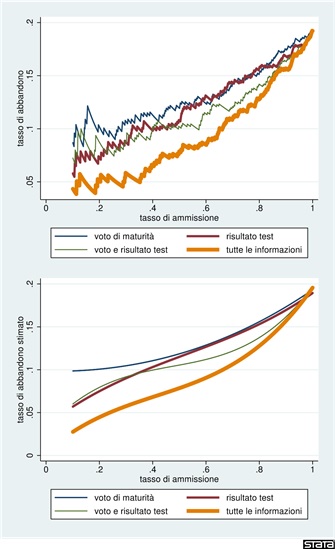
Figura 4.1 Relazione stimata tra tasso di abbandono e differenti criteri di selezione e interpolazione cubica della relazione (secondo grafico). [fonte: banca dati iscritti ed esami sostenuti, Corso di Laurea in Economia, Ancona]

Il primo grafico presenta i risultati stimati, il secondo una interpolazione cubica della relazione stimata.

Per i livelli di ammissione superiori al 50% dei candidati, si pu  notare che se si utilizzano o il voto di diploma o il risultato del test, la qualità della selezione è sostanzialmente la stessa. La validità migliora se i due dati vengono utilizzati congiuntamente.

Le informazioni relative alla probabilità stimata di abbandono per ogni studente, ci permettono anche di valutare l’opportunità di porre in essere un processo di selezione. Il peso da assegnare al numero degli immatricolati rispetto al peso da assegnare al drop out, deve essere veramente basso. Sembra quindi difficile che i corsi di studio trovino ottimale, almeno in un’ottica di breve periodo, scegliere di selezionare gli studenti.

I risultati ci dicono quindi che, se i corsi di studio decidono di effettuare la selezione, è probabilmente perché esiste un numero massimo di immatricolati che possono essere ammessi oppure perché, in un ottica di lungo periodo, si ritiene che la selezione migliori le caratteristiche qualitative del pool di candidati.

Una diversa modalità che secondo i vari criteri di selezione analizzati ci permette di valutare la qualità della selezione si basa sulla comparazione tra gli individui che non verrebbero ammessi all’iscrizione perché ritenutideboli e a forte rischio di abbandono e gli individui che effettivamente hanno abbandonato gli studi. A tal fine, assumiamo che il problema della definizione della quantità ottimale di studenti da ammettere (x*), sia stato risolto dagli organi decisionali del corso di studi massimizzando una qualche funzione obiettivo (così facendo non consideriamo che x* dipende dalla qualità del processo di selezione) oppure a causa di vincoli strutturali. In particolare supponiamo che x* = 555, cioè che la selezione riguardi circa il 19.2% dei candidati (che coincidono con gli studenti che, nella banca dati, hanno effettivamente abbandonato gli studi alla fine del primo anno) e analizziamo quali differenti criteri di valutazione permettano, ex post, di selezionare al meglio i candidati.

Ai fini della selezione dei candidati utilizziamo le stesse variabili indicate nell’elenco 1-5 precedente. Ponendo in essere la selezione, gli organi accademici possono andare incontro ad errori di due tipi:

•    non accettare studenti che non avrebbero abbandonato gli studi;
•    accettare studenti che, di fatto, abbandonano gli studi

La Tabella 4.2 riporta il numero di studenti selezionati in modo errato, come somma dei due errori che è possibile commettere in sede di selezione.

La Tabella presenta anche il valore del test di Pearson ed il suo livello di significatività come indicatore della bontà del criterio di selezione rispetto all’effettivo abbandono. La prima riga considera un criterio di selezione completamente casuale.

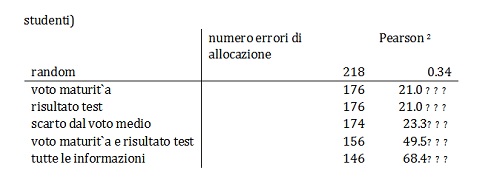
Tabella 4.2 Errori nella selezione con differenti criteri di selezione su 687 studenti. Ipotesi del 19.2% di candidati non ammessi.[fonte: banca dati iscritti ed esami sostenuti. Corso di Laurea in Economia, Ancona]

Dalla tabella non emergono differenze nel numero di candidati ammessi e non ammessi erroneamente, tra la selezione basata sul test e quella basata sul voto. In particolare, sembra che il test non aggiunga nulla rispetto a quanto contenuto nell’informazione derivante dal voto di maturità. Il numero di studenti ammessi erroneamente si riduce, invece, quando le informazioni derivanti dal voto di maturità e dal risultato dal test sono considerate in modo congiunto (di circa il 10% rispetto ad una selezione basata sul solo test o sul solo voto di maturità) e, ancora di più, nel caso in cui vengano utilizzate tutte le informazioni (di circa il 17%). In quest’ultimo caso, la probabilità di errore rispetto ad un criterio completamente causale si riduce di un terzo.  Altre indicazioni relative alla performance degli studenti possono derivare sia dal numero dei crediti formativi universitari (CFU) che dal voto medio agli esami che sarebbero stati ottenuti dagli studenti ammessi, a seconda del metodo di selezione. I CFU rappresentano una proxy (inversa) della durata attesa degli studi mentre il voto degli esami superati al primo anno rappresenta una proxy del voto di Laurea. Per i 5 metodi di selezione visti sopra, la banca dati permette di calcolare il numero dei CFU e del voto medio ottenuto dagli studenti che sarebbero stati ammessi e che non sarebbero stati ammessi.

La Tabella 4.3 riporta i risultati di queste analisi distinguendo tra studenti “non ammessi” e studenti “ammessi”. Tanto maggiore è la differenza in termini di CFU e di voto tra i due tipi di

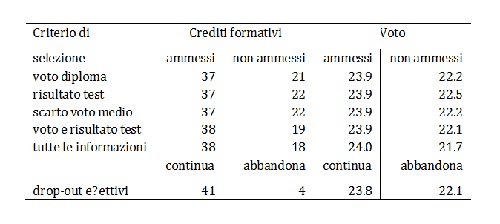
Tabella 4.3 Errori nella selezione con differenti metodi. Ipotesi del 19.2% di candidati non ammessi. [fonte: banca dati iscritti ed esami sostenuti. Corso di Laurea in Economia, Ancona]
studenti, tanto più il criterio di selezione è efficiente. Nell’ultima riga sono presenti informazioni relative ai CFU ed al voto, sia degli studenti che non hanno abbandonato che di quelli che lo hanno fatto. Le varie modalità di selezione sono tutte in grado di differenziare il numero di crediti formativi ottenuti tra coloro che vengono ammessi e coloro che invece non sono ammessi.   Alla luce di questa analisi, si conferma che le migliori selezioni sono o quella che si basa sull’utilizzo congiunto delle informazioni che provengono dal voto di maturità e dal risultato del test di ingresso oppure quella basata su tutte le informazioni disponibili. Ciononostante, emerge che coloro che abbandonano ex-post gli studi (ultima riga), ottengono un numero di crediti molto più basso. Il voto medio ottenuto agli esami non sembra, invece, dipendere dai criteri di selezione utilizzati. Anche considerando coloro che hanno effettivamente abbandonato gli studi, le differenze nei voti medi sono comunque molto limitate.

 

© I predittori della performance accademica  – Laura Foschi